The work of our group is primarily focused on the electron correlation problem - namely how to compute the correlation energy for an atom, molecule, or solid, starting from a mean-field (say Hartree-Fock) description of the system. Our approach is to combine quantum chemical ideas with stochastic (Monte Carlo) techniques, which enable us to tackle problems which are very difficult to solve use standard quantum chemical techniques alone.
We are developing Quantum Monte Carlo algorithms adapted for electronic (and more generally Fermionic) problems by working in Slater determinant spaces. The central problem which is encountered is the infamous "Fermion sign problem", which results from electronic wavefunctions having both positive and negative amplitudes. Currently we are working on a novel population dynamics algorithm which propagates walkers in Slater determinant space according to a type of "stochastic cellular automaton" obeying simple rules. The movie on the home page shows an evolving population of walkers of positive and negative sign settling on the FCI wavefunction of a nitrogen dimer in a minimal basis - an archetypal multireference system. The remarkable aspect of this dynamics is the spontaneous symmetry breaking caused by annhilation processes, allowing the exact nodal surface of the nitrogen molecule, as expressed by the CI coefficients, molecule to appear. No fixed-node approximation is applied.
The original articles describing these algorithms can be downloaded from here - FCIQMC and i-FCIQMC . The technique has been applied to atomic systems including cations and anions , to diatomic molecules , and to the homogeneous electron gas. Applications to real solids are currently being computed.
The movie below shows an example of an FCIQMC simulation for a model of streched N2.
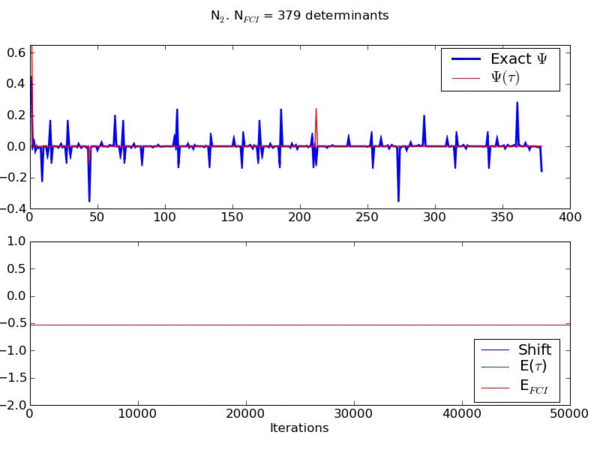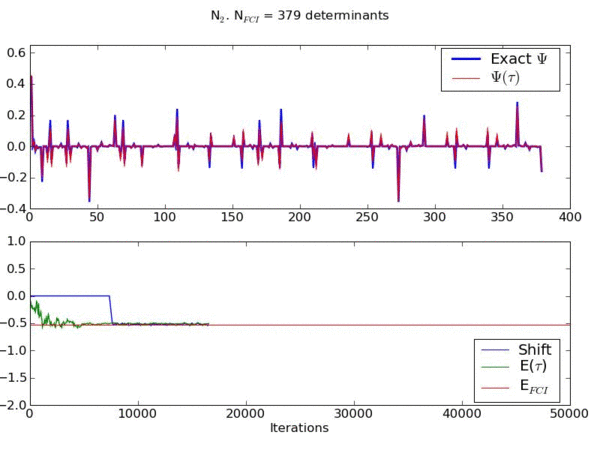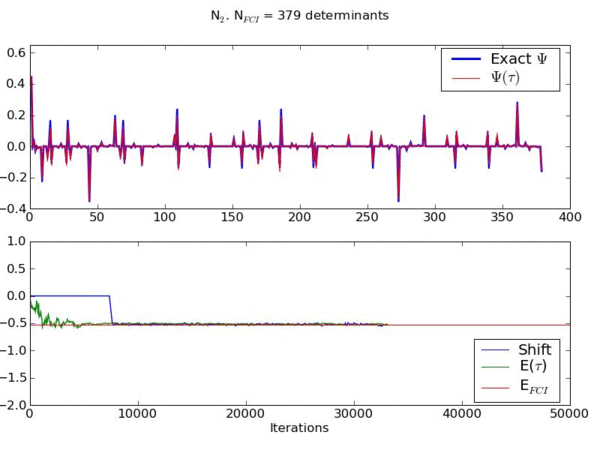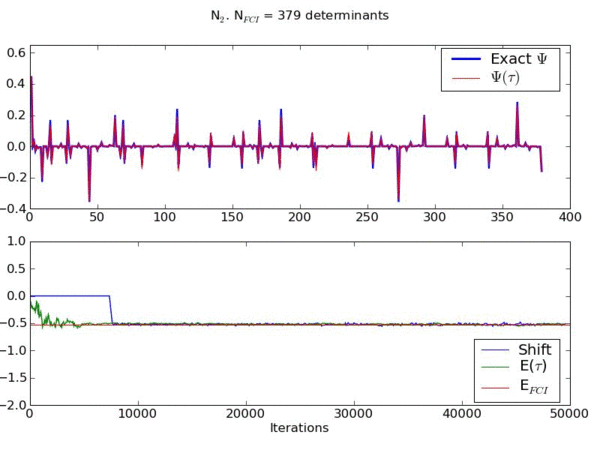
This movie shows the convergence of a wavefunction obtained using a novel stochastic method to the exact ground state wavefunction for the stretched nitrogen molecule in a space of 379 basis functions.
The upper graph shows the contribution of each basis function to the wavefunction (compared to the exact result) as the system evolves. The lower graph shows the energy of the instantaneous wavefunction and the shift (which is another measure of the instantaneous correlation energy) compared to the exact result.