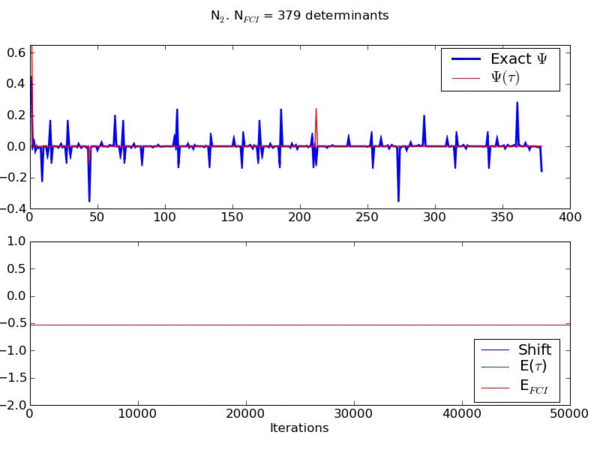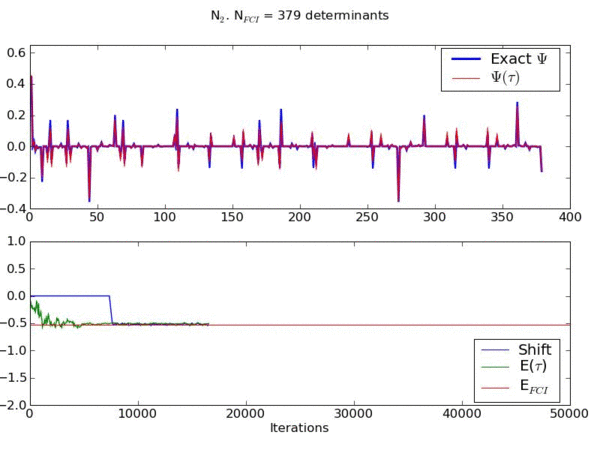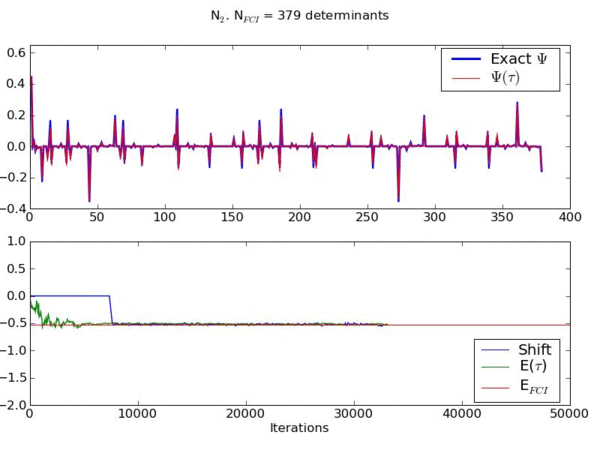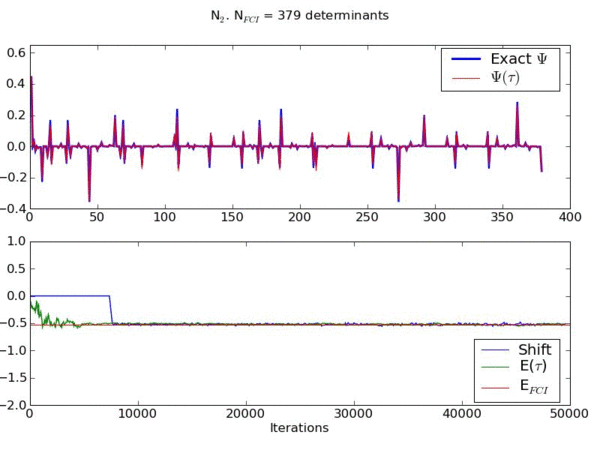
This movie shows the convergence of a wavefunction obtained using a novel stochastic method to the exact ground state wavefunction for the stretched nitrogen molecule in a space of 379 basis functions.

The upper graph shows the contribution of each basis function to the wavefunction (compared to the exact result) as the system evolves. The lower graph shows the energy of the instantaneous wavefunction and the shift (which is another measure of the instantaneous correlation energy) compared to the exact result.

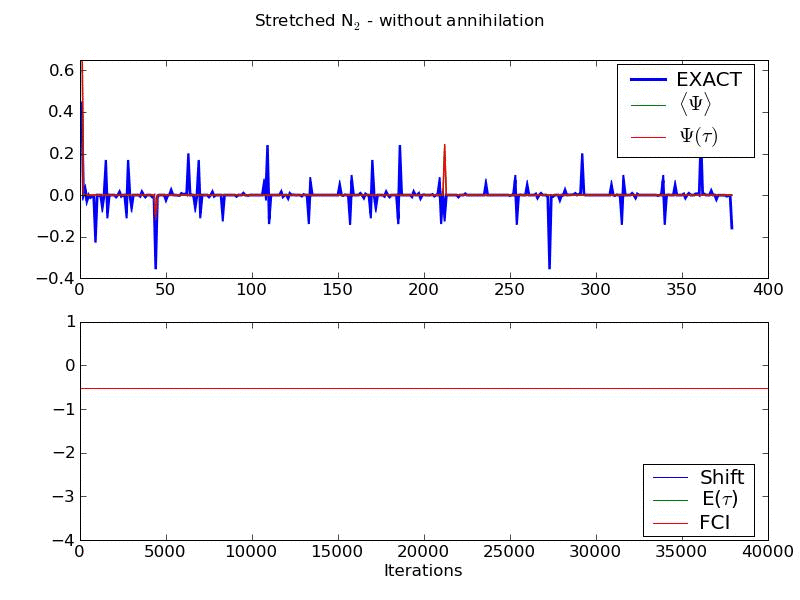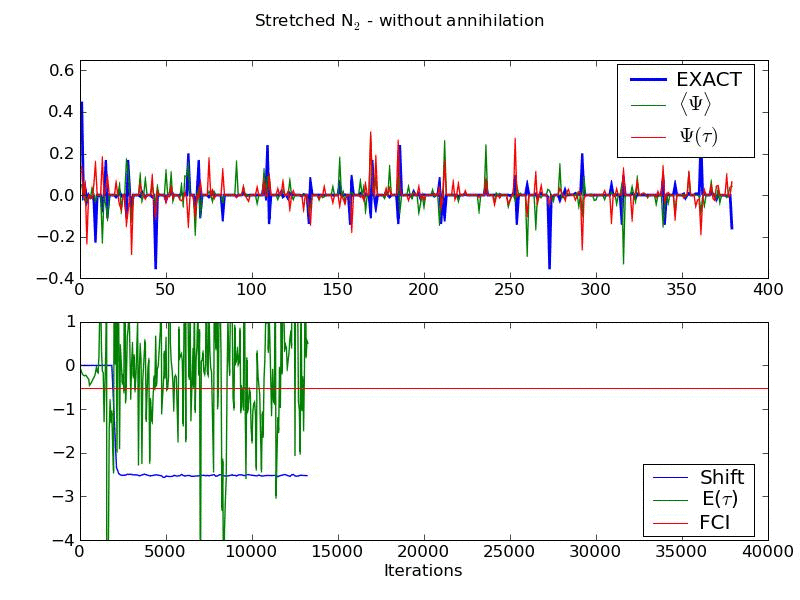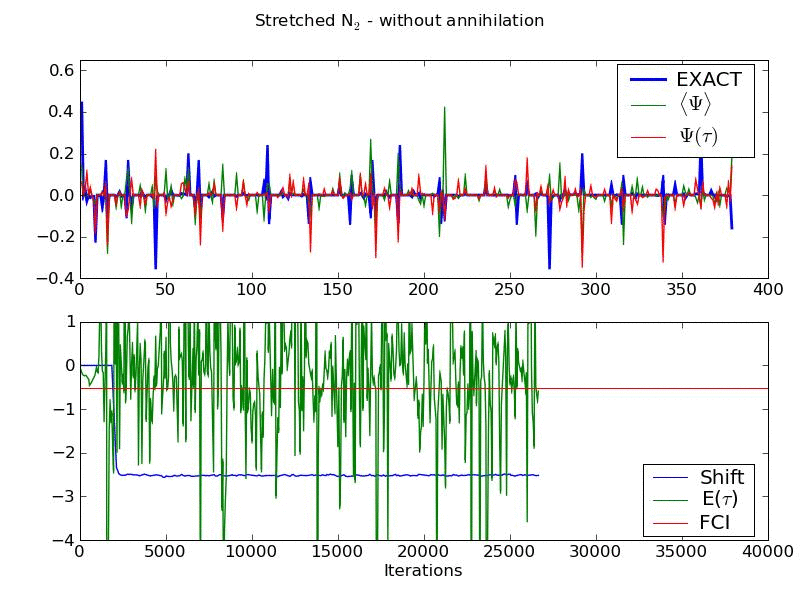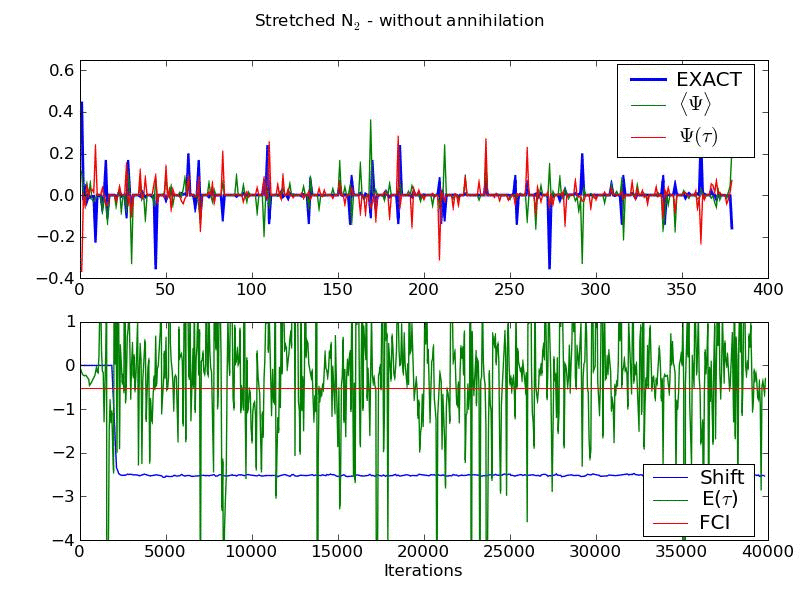
Walker annihilation is found to play a crucial role in allowing the exact nodal surface to be converged upon. Below is an animation of the same system, but with no annihilation step present. It shows an inability to converge the energy or wavefunction, and a value of the shift which stabilises at a much lower value than the true correlation energy. This is a manifestation of the fermion sign problem in our method. Included in the animation is wavefunction averaged over all previous iterations.

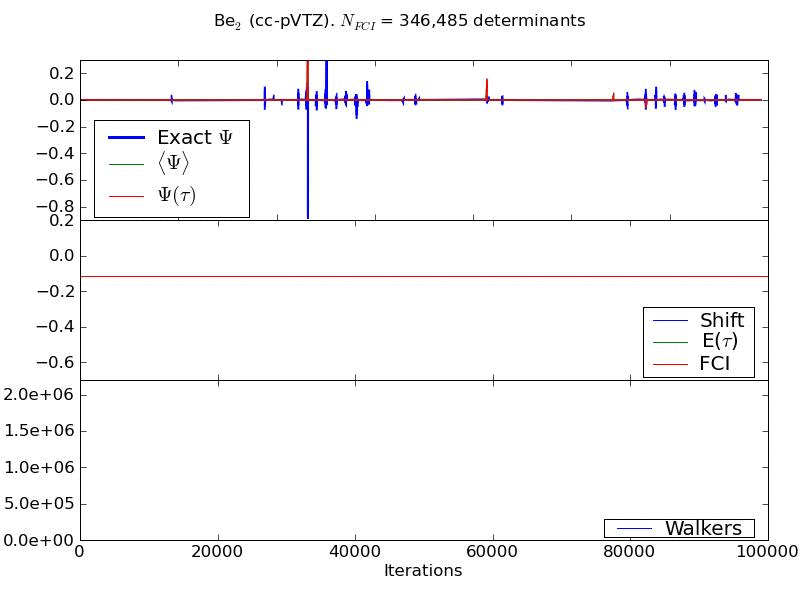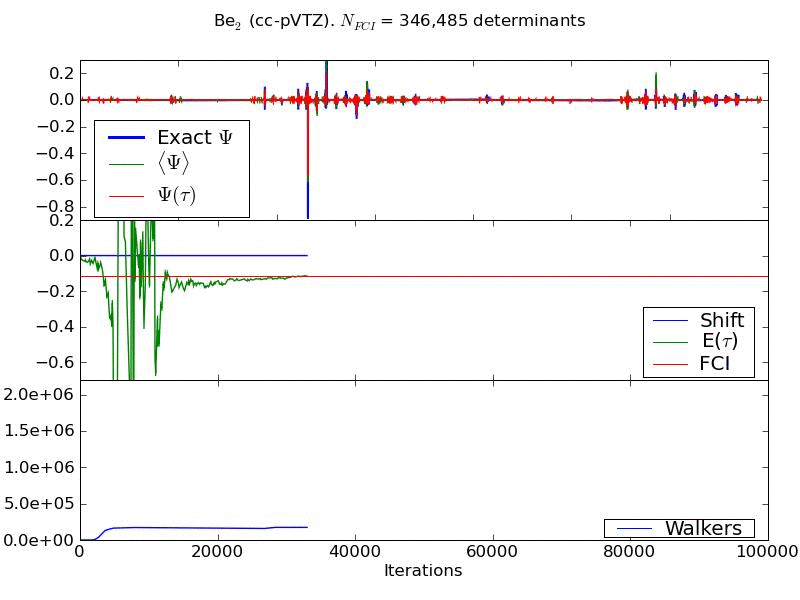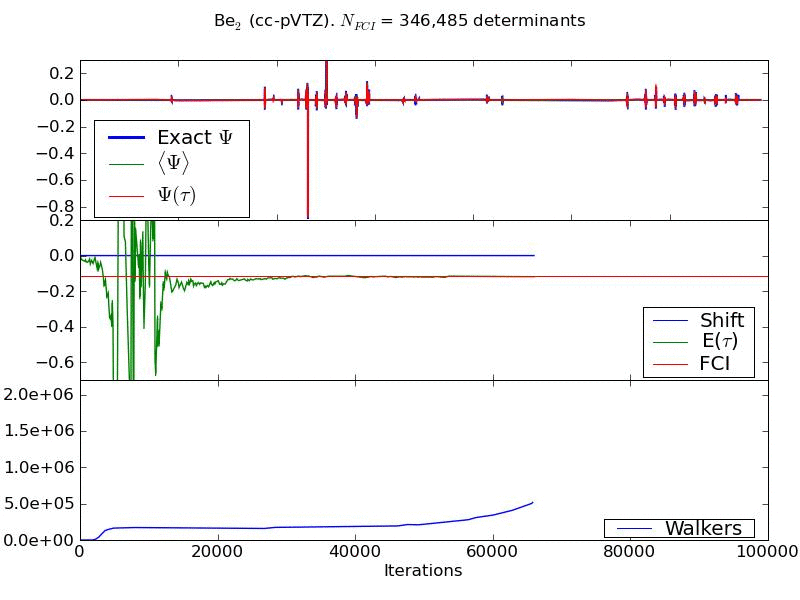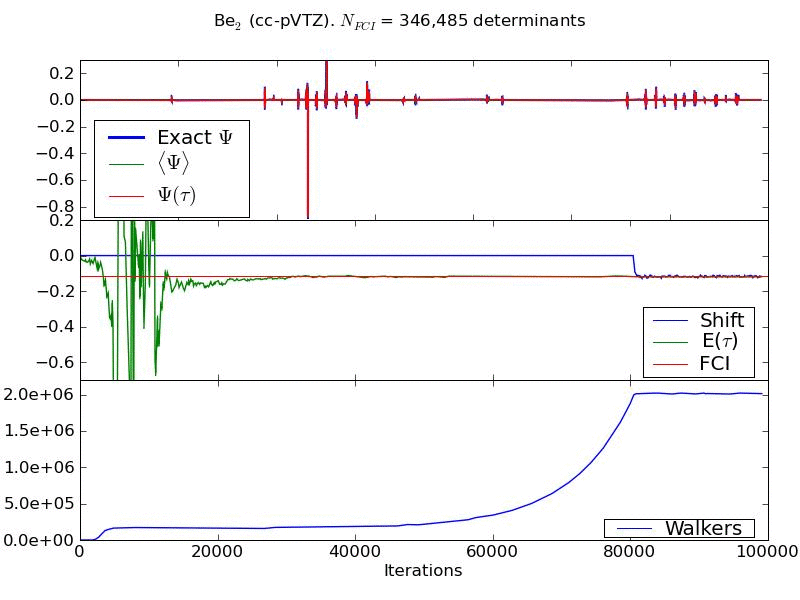
Larger systems can be tackled and have some interesting differences. Below shows the convergence of the wavefunction and energy of a Beryllium dimer in cc-pVTZ basis set. The growth of the walker number is shown in the bottom panel of the animation. During the 'fixed shift' part of the calculation, this number can be seen to plateau at a value of approximately 200,000 walkers. This system-dependant number represents a critical number of walkers, which needs to be attained before the nodal structure of the wavefunction, and hence the energy of the problem, can be correctly converged.

A publication providing more details and results from this method should be available shortly.